Lab - Binary Search Trees

Objectives

• Use and implement binary search trees

• Understand and implement pre, post, and inorder tree traversal

Discussion

There are three main types of tree traversal:

• Preorder - Visit, Left, Right

• Inorder - Left, Visit, Right

• Postorder - Left, Right, Visit

Tree traversal involves performing three specific actions recursively in a specific order:

• Go to left child (Left)

• Go to right child (Right)

• Perform an action (Visit)

These three algorithms are used to implement different parts of a binary tree. For example, as dicussed in lecture, binary trees must be destructed in postorder, and they must be copied in preorder.

To visually understand these traversals, build a tree using this tool (https://tree-visualizer.netlify.app) and see how the three algorithms perform.

These three algorithms work across all binary trees. In addition to these, binary search trees have an efficient way to insert and search for data.

Because binary search trees enforce that any left descendants of a node are less than said node, and any right descendants are greater than said node, searching for a specific data point (or location to insert a data point) is efficient. On average, searching a binary search tree will take log(n) operations, where n is the number of items in the tree. This is an average though - imagine a binary tree which only has right children. This hypothetical tree is essentially just a linked list, and searching that tree will take n operations.

Setup

We need to:

1. Create a directory called binary_tree in your cs23001 folder

2. Copy the btree.hpp file from shared/labs/binary_tree into your binary_tree folder

Assignment

The header file you've been given, btree.hpp contains an incomplete definition of a binary tree. Specifically, it is a binary search tree.

There are three main parts to this assignment:

1. Implement the find, inorder, preorder, and postorder functions.

2. Create a main file called main.cpp. In this file, you need to recreate the following tree by manually calling insert with values in the correct order. It is not enough to insert the same values as the tree, your copy MUST have the exact same structure. After recreating the tree, demonstrate the 4 functions you implemented in Part 1. Make sure to label the output.



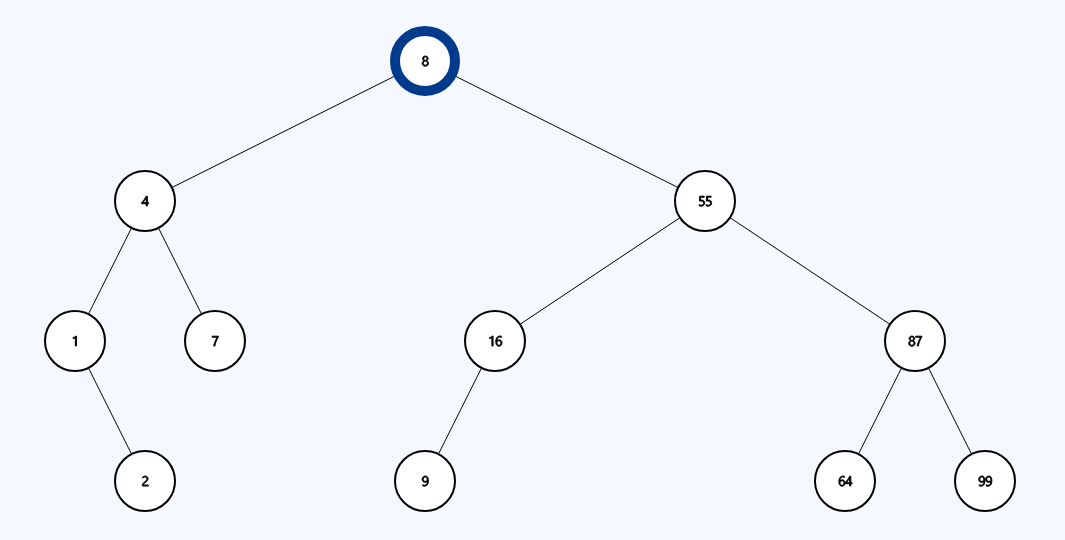
3. Add a new function to the tree, findDepth. This function will work similarly to how find works. However, instead of returning a boolean, this will return an integer denoting the height at which the provided data was found. For example, running findDepth(16) on the above example will return 2. If the data is not in the tree, return -1.

Requirements

The following should be true when you are done, NAMES MUST MATCH EXACTLY:

• In your cs23001 directory you have created a directory named sort_report.

• In the directory binary_tree you have the following files:

• The copied btree.hpp, with your additions.

• main.cpp

• There are NO executables in the repository.